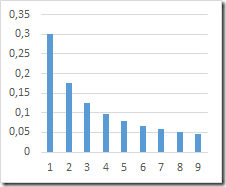
Benford’s law states that in many naturally occurring collections of numbers the small digits occur disproportionately often as leading significant digits. For example, in sets which obey the law the number 1 would appear as the most significant digit about 30% of the time, while larger digits would occur in that position less frequently: 9 would appear less than 5% of the time.
The leading digit “d” tends to have the probability of Log10(1+1/d):
Since statistical and financial data often obeys the Benford’s law it is a widely accepted fraud detection method to compare the distribution of leading digits with the theoretical distribution.
Fortunately it is pretty easy to implement the Benford’s analysis in the OLAP cubes.
Here are the extentions of an existing multidimensional SSAS solution:
- New dimension “First Digit” (1,2,3…9)
- For every measure/column to be analysed its measure group becomes a new key referencing the dimension “First Digit”
- Calculated members in cube script which bring the analysis in the handy form
Implementation steps for Adventure Works
1. Let’s define the new dimension First Digit with the following query in DataSourceView:
SELECT 1 AS ID, ’1…’ AS Name UNION ALL
SELECT 2 AS ID, ’2…’ AS Name UNION ALL
SELECT 3 AS ID, ’3…’ AS Name UNION ALL
SELECT 4 AS ID, ’4…’ AS Name UNION ALL
SELECT 5 AS ID, ’5…’ AS Name UNION ALL
SELECT 6 AS ID, ’6…’ AS Name UNION ALL
SELECT 7 AS ID, ’7…’ AS Name UNION ALL
SELECT 8 AS ID, ’8…’ AS Name UNION ALL
SELECT 9 AS ID, ’9…’ AS Name
The single attribute of the dimension will look like following:
2. Now let’s assume that we want to analyse the SalesAmount from Reseller Sales.
The measure group becomes a new dimension key SalesAmount_FirstDigit defined as:
CAST(LEFT(CAST(ABS(SalesAmount) AS NVARCHAR(32)), 1) AS INT)
Don’t forget to define a regular relashionship between Dimension “First Digit” and the correspondent measure group in cube using the key SalesAmount_FirstDigit.
We take the measure [Reseller Transaction Count] as base value for our statistics.
3. We define the calculated measures to be able to compare the distributions visually as well as to run a statistical assessment formally (using Kolmogorov–Smirnov test).
Please see the inline comments for details.
// —————————–
// Benford’s analysis (BEGIN) –
//——————————
//
// Change the definition of [Measures].[First Digit Count]
// if you want to analyse another measure group.
Create Member CurrentCube.[Measures].[First Digit Count]
as
[Measures].[Reseller Transaction Count]
,DISPLAY_FOLDER=’Benford”s analysis’;
// Distribution of the first digit in data
Create Member CurrentCube.[Measures].[First Digit Count %]
as
[Measures].[First Digit Count]/
([Measures].[First Digit Count],[First Digit].[First Digit].[All])
,Format_String = “Percent”, DISPLAY_FOLDER=’Benford”s analysis’;
// Theoretical distribution
Create Member CurrentCube.[Measures].[First Digit Benford %]
as // Use constants for performance!
VBA/VBA
,Format_String = “Percent”, DISPLAY_FOLDER=’Benford”s analysis’;
// Exception for [All]
([Measures].[First Digit Benford %],[First Digit].[First Digit].[All])=1;
Format_String([Measures].[First Digit Benford %])=”Percent”; // format correction
// Cumulative value for Kolmogorov–Smirnov test
Create Member CurrentCube.[Measures].[First Digit Count % Cumul]
as
[Measures].[First Digit Count %]
+[First Digit].[First Digit].currentmember.prevmember
,Format_String = “Percent”, DISPLAY_FOLDER=’Benford”s analysis’;
// Recursion seed
([Measures].[First Digit Count % Cumul],[First Digit].[First Digit].&[1])
=[Measures].[First Digit Count %];
Format_String([Measures].[First Digit Count % Cumul])=’Percent’; // format correction
// Cumulative value for Kolmogorov–Smirnov test
Create Member CurrentCube.[Measures].[First Digit Benford % Cumul]
as
[Measures].[First Digit Benford %]
+[First Digit].[First Digit].currentmember.prevmember
,Format_String = “Percent”, DISPLAY_FOLDER=’Benford”s analysis’;
// Recursion seed
([Measures].[First Digit Benford % Cumul],[First Digit].[First Digit].&[1])
=[Measures].[First Digit Benford %];
// Exception for [All]
([Measures].[First Digit Benford % Cumul],[First Digit].[First Digit].[All])=1;
Format_String([Measures].[First Digit Benford % Cumul])=”Percent”; // format correction
// The Kolmogorov–Smirnov statistic (D)
Create Member CurrentCube.[Measures].[First Digit Cumul Delta to Benford]
as
IIF([Measures].[First Digit Count % Cumul]=0,NULL,
ABS([Measures].[First Digit Benford % Cumul]-[Measures].[First Digit Count % Cumul]))
,Format_String = “Percent”, DISPLAY_FOLDER=’Benford”s analysis’;
// The goodness-of-fit Kolmogorov–Smirnov test (SQRT(N)*D)
Create Member CurrentCube.[Measures].[First Digit K-S Test]
as
MAX([First Digit].[First Digit].[First Digit],[Measures].[First Digit Cumul Delta to Benford])
*
VBA)
,Format_String = “#.00″, DISPLAY_FOLDER=’Benford”s analysis’;
// —————————–
// Benford’s analysis (END) –
//——————————
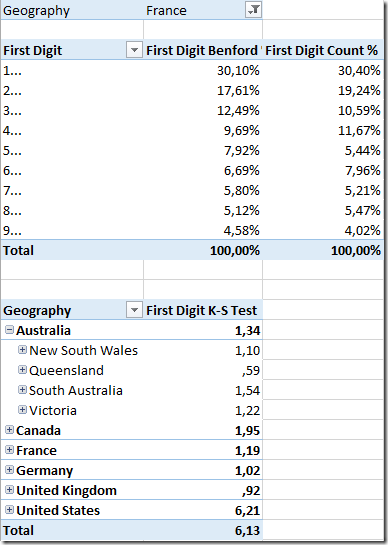
Sample results
The analysis in tabular form in Excel:
The larger the “K-S Test”, the more probable that the data does not obey the Benford’s law (see table of critical values here).
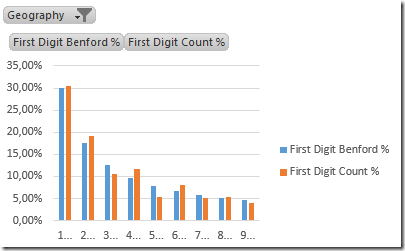
The graphical analysis could look like:
Here the data for France shows a pretty good fit (K-S Test = 1,19).
Implementation notes
- The MDX here is not performance optimized. You can start with using precalculated constants for [First Digit Benford %].
- You can make some of calculated measures invisible. For instance cumulative ones.
- Here we made only one measure available for Benford’s analysis. To analyze further measures/columns you have to define more keys for dimension First Digit in your tables and add a selector dimension for the [First Digit Count] (unrelated to data) and do the switching in your cube script. If you have more than one measure/column to analyse per measure group, you have to define a role playing dimensions based on the dimension First Digit.
Warning
Of course you don’t have to expect, that every data obeys the Benford’s law. Please refer to the corresponding topics and go through references here.